gulden snede

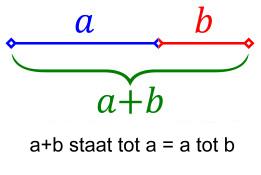
De gulden snede bevat twee delen in de verhouding 8:5 (exacter is het 1,618:1). Over de gulden snede wordt in de architectuur vooral gesproken als men de verdeling van bouwdelen in de verhouding 8:5 toepast, wat visueel een evenwichtiger beeld kan geven.
De gulden snede wordt aangeduid met de Griekse letter F (phi, [fi]); dit is het getal 1,6180339887... of (1+√5)/2, maar dat we gemakshalve als 8/5 aangeven.

Een gulden rechthoek is een rechthoek met de verhouding lengte/breedte van 8:5. Bij de foto van de schelp Nautilus geven de windingen een gulden spiraal uit de gulden rechthoek. Een gulden rechthoek min een vierkant is een tweede gulden rechthoek. Van deze gulden rechthoek kan weer een vierkant worden afgetrokken enz.

In een algemene formule: 
lengte / breedte = (lengte+breedte) / lengte.

De oude Grieken hebben de gulden snede toegepast voor de visueel meest aangename verhouding tussen bouwdelen.

In de afbeelding die Vitruvius van een mens maakten de uitgestrekte lichaamsdelen de gulden snede.

de gulden snede wordt in een lijnvorm aangegeven door de volgende afbeelding;  in een rechthoek geldt lengte a staat tot breedte b = (a+b) staat tot a:

bij onderstaande tekening is lijn DC:AD = 1,618:1 (ofwel vrijwel 8:5):

gulden spiraal van de nautilus schelp:

en de nautilus in geometrische vorm:

Grappig is:
F = (1+√5)/2 dus
F = 1,6180339887498948482045868343656...

F² = 2,6180339887498948482045868343656...

1/F = 0,6180339887498948482045868343656...

en
6*(1+F )/5 = 3,141640786 is vrijwel gelijk aan p (pi)

Zie ook geometrische figuren, module en Bossche School.
Afbeeldingen o.m. Wisfaq en Wikipedia (user Stannered).

Eng. golden ratio, golden section, golden mean