1. Significant betekent in het algemeen belangrijk (vaak verhoudingsgewijs belangrijk). Bijvoorbeeld in de zin "Significante afwijkingen" zijn het afwijkingen die belangrijk zijn voor de bepaling van iets en dus zeker niet weggelaten kunnen worden. Anderzijds kunnen we soms kleine waarden weglaten omdat die in het totaalplaatje geen enkele betekenis hebben. We laten in zo'n geval de niet-significante gegevens weg. *)
2. Significant geeft bij natuurkunde en scheikunde en daarmee ook vaak in de bouwkunde aan hoe nauwkeurig een getal is. Bijvoorbeeld het getal 56 is in twee cijfers significant, net als bijvoorbeeld het getal 5,6 en de getallen 0,56 en 0,056.
Significantie geeft dus ook aan hoe nauwkeurig een getal is, niet te nauwkeurig ("teveel cijfers achter de komma") maar ook niet te globaal (getal uitgedrukt in te weinig cijfers).
Bij een berekening met een aantal getallen geldt: het getal met de laagste nauwkeurigheid geeft de significantie aan van het eindresultaat. Wanneer het getal met het kleinste aantal cijfers in 2 cijfers nauwkeurig is en de rest van de getallen is in 5 cijfers nauwkeurig, dan is een eindresultaat in 5 cijfers veel te nauwkeurig en verliest daarmee zijn betekenis. We geven bij voorkeur de uitkomst niet nauwkeuriger dan het kleinste aantal cijfers van de getallen die meespelen.
Opmerkingen
- Verwarring kan ontstaan als een decimale nul wordt weggelaten: een gemeten waarde van 3,1 is in 2 cijfers nauwkeurig, maar als de gemeten waarde eigenlijk 3,10 is dan kan het eindresultaat ook in 3 cijfers nauwkeurig bepaald worden (mits de overige getallen ook in minimaal 3 cijfers gegeven zijn). Ook de decimale nul achteraan heeft dus zeker waarde.
- Bij kleine getallen is de significantie nog belangrijker dan bij grote getallen: een gemeten waarde van 1,2 kan wellicht 1,15 of 1,25 zijn (een variatie van 0,1 op 1,2 dus ca. 8% afwijken), terwijl een gemeten waarde van 8,2 kan liggen tussen 8,15 en 8,25 met een variatie van 0,1 op 8,2 dus ca. 1%.
- Zorg dat cijfers zo nauwkeurig mogelijk zijn bepaald.
Een paar voorbeelden
- In een krant is sprake van de aanleg van een tijdelijk fietspad voor "ongeveer 591.555 euro" waarbij ook nog eens van een "grove raming" sprake is. Zowel een ongeveer-bedrag als een (al of niet grove) schatting mogen natuurlijk nooit zo nauwkeurig zijn. Of de wethouder met dit onzinnig nauwkeurige ongeveer-bedrag kwam is niet zeker, maar de redacteur had toch wel iets minder significant mogen zijn.
het stukje uit het algemeen dagblad van 29 maart 2023: |
- De waarde van hout in een bepaald bos werd, wanneer de bomen volgroeid zijn, geschat op 910.225 euro. De onzekerheden en onnauwkeurigheden zijn hier o.m.:
(a) de tijd tot volgroeid zijn van de bomen duurt nog een (onbekend) aantal jaren (mede afhankelijk van het weer)
(b) de prijs van boshout fluctueert meestal fors
(c) onduidelijk is om hoeveel bomen het precies gaat
(d) niet alle bomen worden gelijktijdig volwassen
(e) de kosten van herplanten staat niet vermeld bij de opbrengst en dat kost misschien in de toekomst veel meer (of wellicht juist minder).
Er zijn dus veel factoren waardoor de prijs op enig moment onzeker is. Een waarde van 910.225 euro is in dit geval veel te nauwkeurig ofwel veel te significant. Misschien dat "ca. 1 miljoen euro" reëel is (met de toevoeging dat we helaas niet in de glazen bol van de toekomst kunnen kijken).
- Als je twee gemeten waarden hebt, de eerst 1,217 en de tweede 3,1 dan kun je bij vermenigvuldiging als resultaat 3,7727 hebben. Maar 3,1 kan meestal evengoed 3,05 als 3,15 zijn en de 7 van 1,217 is ook onzeker. De uiteindelijke waarde ligt meestal ergens tussen 1,2165*3,05 en 1,2175*3,15 dus tussen 3,71 en 3,84. Afronden van die hypothetische en te nauwkeurige waarde van 3,7727 naar 2 getallen geeft in dit geval 3,8.
Als er zeer nauwkeurig gemeten is, en de waarde is 3,10 dan is een uitkomst in 3 cijfers reëel (3,77 wordt het dan).
- Bij de berekening van de benodigde capaciteit van de verwarming van een grote woonkamer werd bijvoorbeeld een getal van 6523 W gegeven, wat complete onzin is als er zoveel factoren zijn die niet zo nauwkeurig bepaald kunnen worden (onzekerheid werkelijke isolatiewaarde van het glas, kieren bij deuren, open keuken, wel/geen deur naar de trap enz.). 6500 W of 7000 W (neem bij voorkeur altijd een wat grotere capaciteit bij verwarming en soms ook koeling) zijn reëlere getallen.
- Bij bepaling van de warmtecapaciteit van een materiaal als rubber met een niet geheel bekende soortelijke massa van 1200-1600 kg/m3 en een gestelde soortelijke warmte van 1,47 kJ/kgK levert dit berekende warmtecapaciteiten op van 1764-2352 kJ/m3K wat natuurlijk veel te nauwkeurig is met die brongegevens (1200-1600 verschilt nogal van elkaar en 1,47 in 3 cijfers is dan veel te nauwkeurig). Dan zou 1750-2350 of 1700-2400 een reëler bereik zijn.
- Uit een onderzoek/rapport van de GGD "blijkt" dat de kans op borstkanker toeneemt als je zeer vaak je handen wast met een desinfectiemiddel met ethanol (alcohol). Die vergroting van de kans is echter slechts 0,012%... Natuurlijk is elk geval minder toe te juichen en natuurlijk is het niet goed als je enorm vaak je handen met wat voor middel dan ook wast en moet je andere mogelijkheden aangrijpen (steeds handschoenen gebruiken en elke keer verversen), maar zo'n belachelijk kleine risicovergroting is statistisch pure onzin.
- Het Klimaatfonds levert slechts 0,000036 graden C voordeel op (je moet echt even de nulletjes tellen achter de komma).
Zo'n voordeel is compleet irrelevant voor het klimaat. Als je dat niet begrijpt (zoals veel politici), dan moet je geen getallen gebruiken en zeker geen dure en ingrijpende politiek daaraan koppelen. Zie dat onderdeel bij groene dwang.
- Een berekening van de kosten en besparingen van een warmtepomp levert een besparing van gas op van 576.57250796755 m3 (decimale punt), terwijl de brongegevens alle zéér veel variaties vertonen binnen de parameters (isolatiegraad muren/vloeren/dak, soort dubbelglas, aantal personen in huis, slappe of strenge winter enz. enz.). De website-software-engineer had hier een bepaalde afronding moeten toepassen, maar er wordt vaak simpelweg niet aan gedacht om dat te doen. (Het extra stroomverbruik van 1699 kWh is even onzinnig nauwkeurig.)
 |
- Een boek over de architectuur van door vogels zelf gemaakte vogelnesten is vertaald uit het Engels en de vertaler worstelt met het omzetten van inches naar centimeters. Een vogelnestje met een nestkom van 1,5 inch diameter wordt dan 3,75 cm. Dat is véél te nauwkeurig: zo'n nestje is misschien 3 cm of 4 of nog wat groter, maar nooit kun je 3,75 cm aangeven.
(Overigens, het boek is reuze-interessant als je belangstelling hebt voor bouwen en architectuur, maar de zeer summiere woordenlijst achterin geeft uitleg over termen die vrijwel iedereen kent en behandelt geen termen die puur vogelaars-jargon zijn. De Vogelbescherming wordt prominent genoemd op de cover en elders, maar waarschijnlijk uitsluitend door een geldelijke bijdrage en niet door het napluizen van de inhoud. Jammer, een gemiste kans.)
 |
- Een grafiek toont uitsluitend het "bovenste" deel van de grafiek waardoor de verschillen veel belangrijker lijken dan ze zijn. (De nul-lijn van de y-as wordt niet getoond in de grafiek waardoor de verschillen vaak veel groter lijken.)
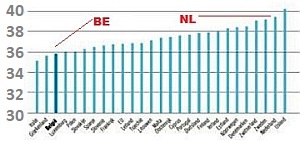 |
Kritische noot
Significantie heeft ook te maken met wat redelijk is. Mensen die weinig begrip hebben van getallen, hebben het daar altijd moeilijk mee en laten zich snel meeslepen door extreme overdrijvingen. Omdat we tegenwoordig zo goed kunnen meten, hebben we ons gevoel voor verhoudingen verloren (met dank aan journalist/chemicus Simon Rozendaal). Daardoor denken veel mensen dat elke waarde slecht is voor onze gezondheid, die waarde kan immers gemeten worden. De normen voor vervuiling worden steeds minder afgestemd op wat werkelijk schadelijk is, maar op wat gemeten kan worden. Het wensdenken van milieumensen (vaak niet de beste getallenkrakers) ligt daar veelal aan ten grondslag.
Overigens, in het Vlaamse Campus Vesta in Ranst is in drie maanden tijd tweederde van de PFAS uit de grond gehaald door die grond te bebouwen met hennep. Daar zullen de milieubewegingen niet blij mee zijn, want dan kunnen ze dat ook niet meer als reden aanvoeren om woningbouw e.d. te dwarsbomen. (...) In Charleroi en Vlaanderen wordt geprobeerd om met PFAS vervuilde grond schoon te maken met hennep, schrijft Vilt.be. Volgens het Algemeen Dagblad loopt in Zeeland een proef om PFAS via oxidatie uit afvalwater te halen. Brits onderzoek toont aan dat bepaalde bacteriën in de menselijke darmen PFAS absorberen en afvoeren. (Waals Weekblad 3 jan 2025, 11 jul 2025)
Significant betekent letterlijk veelbetekenend, afkomstig uit het Latijnse significans (2e nv. significantis), van het werkwoord significare (een teken geven, aanduiden), van signum (teken) en -ficare, een nevenvorm van facere (in samenstellingen -ficere) (maken, doen); bron Etymologiebank.
Zie eventueel ook redundant.
Eng. significant; Du. signifikant; Fr. signifiant
3. In de statistiek wordt met significantie bedoeld dat een gevonden resultaat waarschijnlijk niet op toeval berust, maar dat er een bepaalde statistische samenhang of verband is (correlatie) tussen de waarden.
*) In veel onderzoeken worden belangrijke zaken juist niet meegenomen omdat dat ongunstig is voor het vaak van te voren gewenste resultaat.
(a) Niet alleen bij commerciële onderzoeken gaat dat zo, ook veel wetenschappers houden er stokpaardjes op na waardoor significante aspecten bewust worden weggelaten. Bijvoorbeeld de duurzaamheid van kweekvlees wordt wel eens betwijfeld, maar een paar aspecten worden dan vaak vergeten: er zijn nauwelijks koeien, varkens of kippen nodig dus het ammoniak-probleem (stikstofprobleem) is opgelost en er komt veel land vrij voor woningbouw. (Overigens is het "stikstofprobleem" ook geen echt probleem, maar waarschijnlijk geschapen door mensen die te weinig echte zaken om handen hebben. Zo zijn er ook "experts" die het dragen van een mondkapje als schijnzekerheid bestempelen, terwijl het de enige manier is om jezelf als burger nog een heel klein beetje te wapenen tegen een pandemie. De volhardendheid waarmee de "experts" het mondkapje af bleven wijzen, is verontrustend en een teken dat politici en "wetenschappers" zelfs in erbarmelijke tijden meer met hun ego bezig zijn dan met de gezondheid en het welzijn van de burgers.)
(b) Een ander voorbeeld van opzettelijk negéren van een groot deel van de populatie. Een Woningstichting wil 75 arbeiderswoningen van meer dan 100 jaar oud slopen omdat volgens haar renovatie te duur wordt. Aan een aantal bewoners wordt gevraagd "Kunt u mee in ons voorstel om sloop/nieuwbouw te onderzoeken?" Volgens de communicatieadviseur van de Woningstichting kozen 34 bewoners voor sloop en 15 tegen sloop (dus voor renovatie).
Volgens een onderzoek van de Bewonerscommissie zijn van de 67 ondervraagde huishoudens 17 voor sloop en 50 tegen sloop (soms na enig wikken en wegen).
Aspecten:
- De vraag van de Woningstichting gaat over onderzoeken, niet of de ondervraagde daadwerkelijk achter sloop/nieuwbouw staat! De vraagstelling is extreem belangrijk bij enquêtes, zelfs een ontkennend of bevestigend gestelde vraag speelt een grote rol, en helemaal een dubbel ontkennende vraag ("ontkent u dat u er geen enz."). Vaak wordt de vraag niet specifiek genoeg gesteld, maar zijn de vragen (en dus ook de antwoorden) voor meer uitleggen vatbaar. Simpelweg "Bent u tevreden met de hoogte van enz." houdt bij "ontevreden" niet in dat iemand het hoger wil hebben maar dat het ook juist lager kan zijn. En een vraag als "Hoe klein denkt u dat de kans is enz." houdt al in dat de ondervraagde de kans klein moet vinden en niet groot. Ook vragen met "nooit", "altijd" e.d. kunnen eigenlijk niet beantwoord worden omdat er bijna nooit sprake is van zo'n definitief antwoord. En wat wordt verstaan onder "vaak".
- Onbekend is of de vragen aan specifieke bewoners is gesteld, of meer bewoners uit hetzelfde gezin. Steeds had (alleen) de hoofdbewoner / wettelijke huurder ondervraagd moeten worden.
- Het aantal ondervraagde bewoners is toch nog vrij klein, zeker bij het onderzoek van de Woningstichting.
- De Woningstichting had het over "een deel van de bewoners" dat tegen sloop was. De term "een deel van" heeft voor het gevoel iets kleins in zich, een onbelangrijk deel van het totaal (en daar maakt de Woningstichting natuurlijk gebruik van), maar kan best 80% zijn, of 99%.
- Voor de woningstichting sprak de communicatieadviseur, die functie alleen al, dan weet je zeker dat je als burger op je hoede moet zijn.